一、Regression
回归(Regression),指研究一组随机变量(Y1 ,Y2 ,…,Yi)和另一组(X1,X2,…,Xk)变量之间关系的统计分析方法,又称多重回归分析。通常Y1,Y2,…,Yi是因变量,X1、X2,…,Xk是自变量。
我们这里研究的是线性回归(Linear Regression),说人话就是,线性回归分析是根据一个或一组自变量(X1,X2,…Xk)的变动情况预测与其相关关系的某随机变量(Y)的未来值的一种方法
线性分析是AI中经常运用到的技术
线性回归的例子也有很多,比如预测股票市场(输入前10年的股票行情,输出当前股票的预测情况),无人车驾驶(输入各种道路信息,输出方向盘旋转角度)、推荐系统(输入使用者和商品,输出购买的可能性)
以预测宝可梦的进化后战力为例子
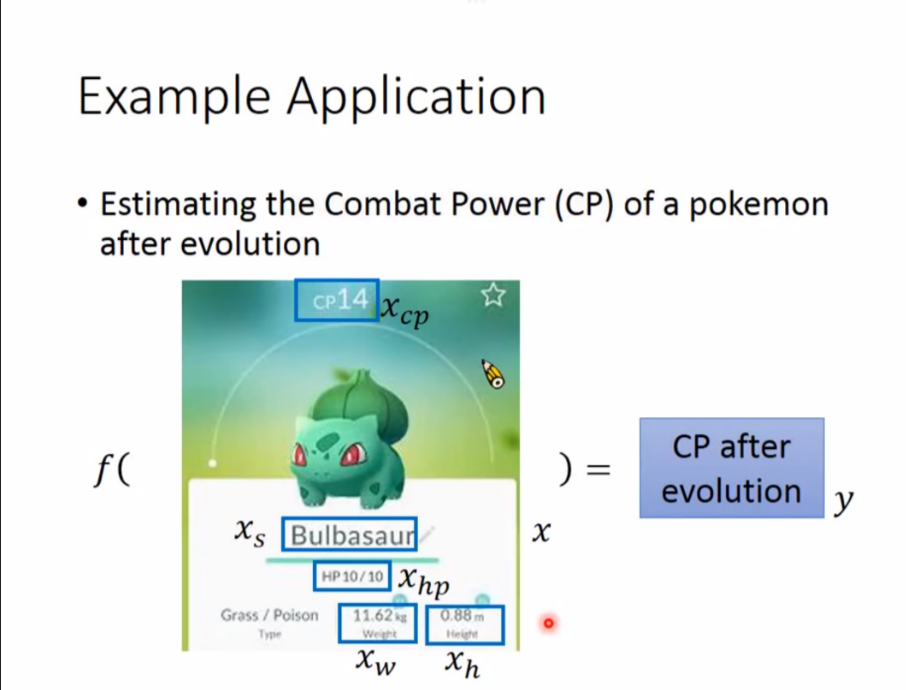 总共可以分成3个步骤
总共可以分成3个步骤
1. Model
第一步是确定模型
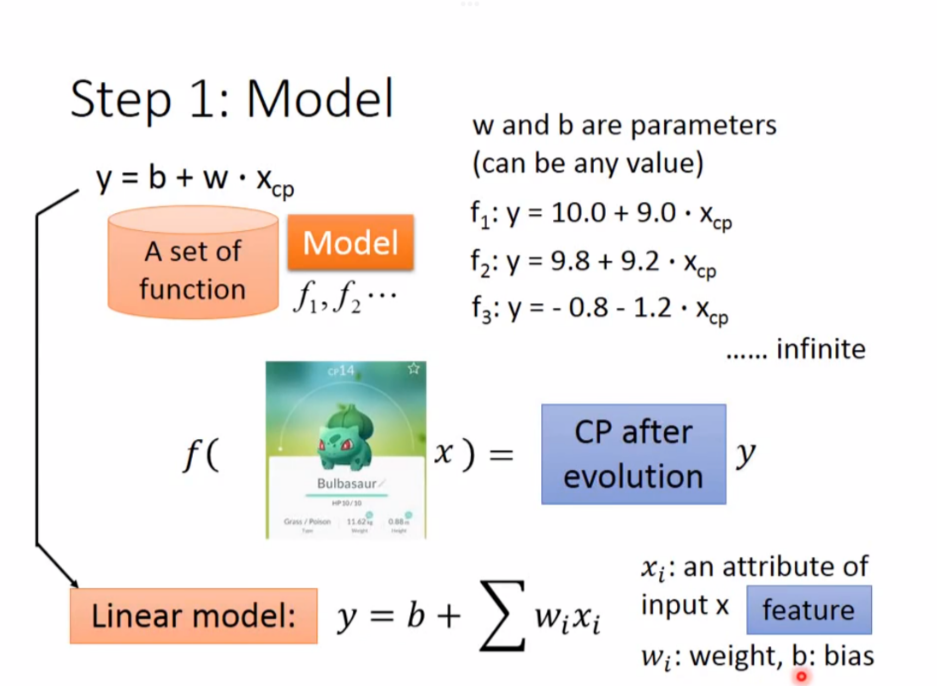 假定一个模型
假定一个模型
$y = b + w*x_{cp}$
2. Goodness of Function
第二步是判断函数的好坏
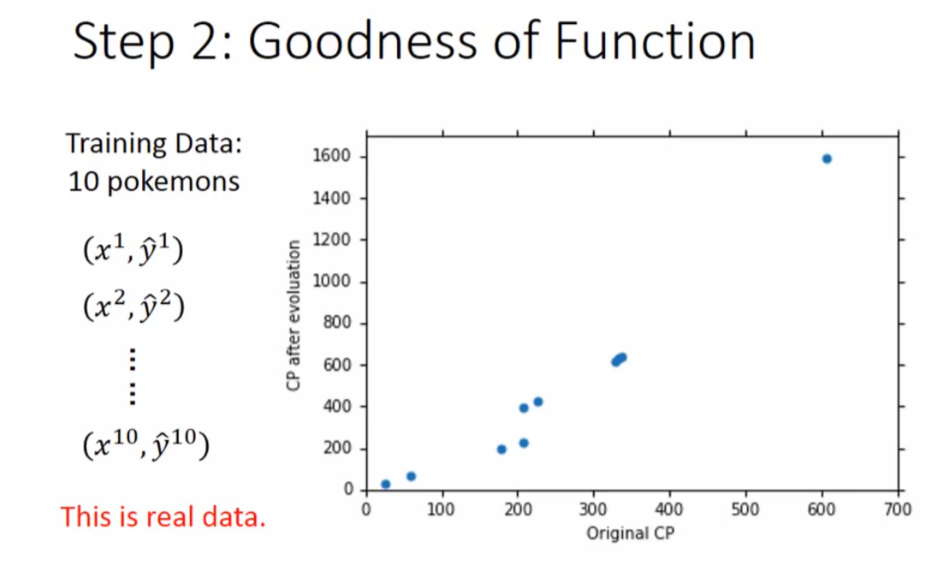

判断函数好坏有一个叫做 Loss Function(输入是一个函数,输出一个函数的好坏)的东西,其实是衡量一个函数是否优秀的标准,其实就是求方差
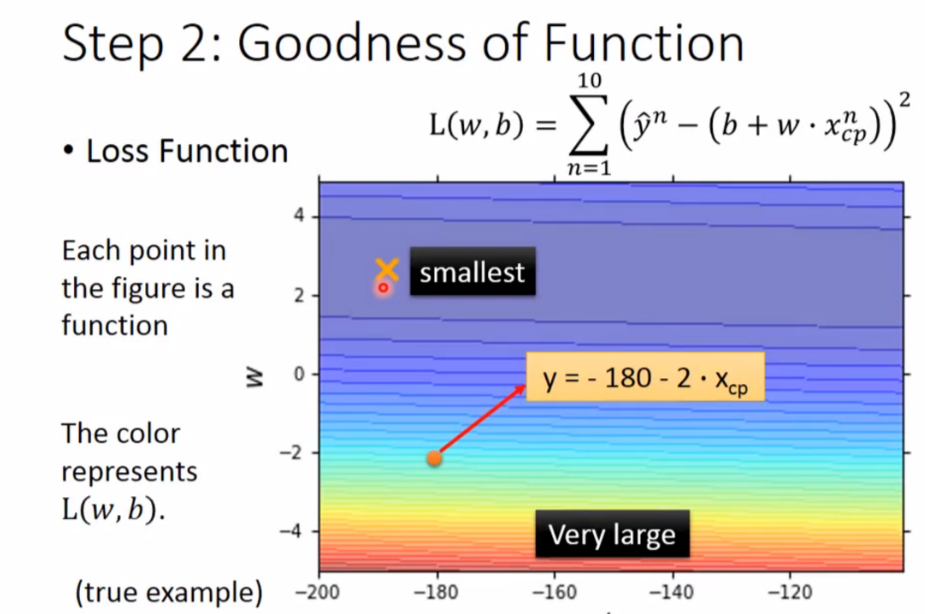
3. Best Function
第三步是找到一个最好的函数
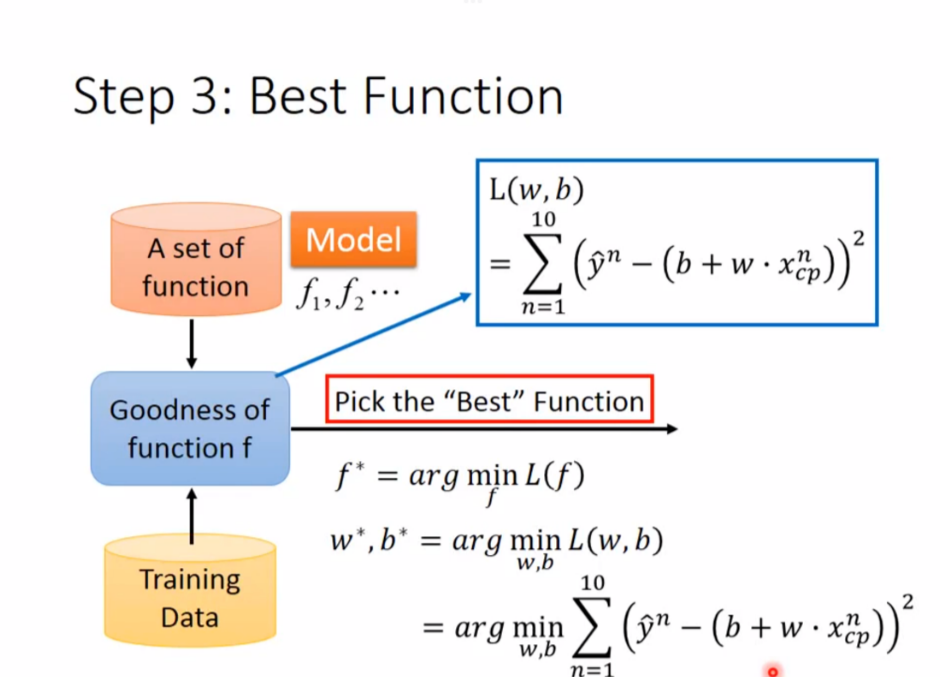 那么如何找到最好的那个函数呢
那么如何找到最好的那个函数呢
这里使用了 Gradient Descent(梯度下降) 的方法
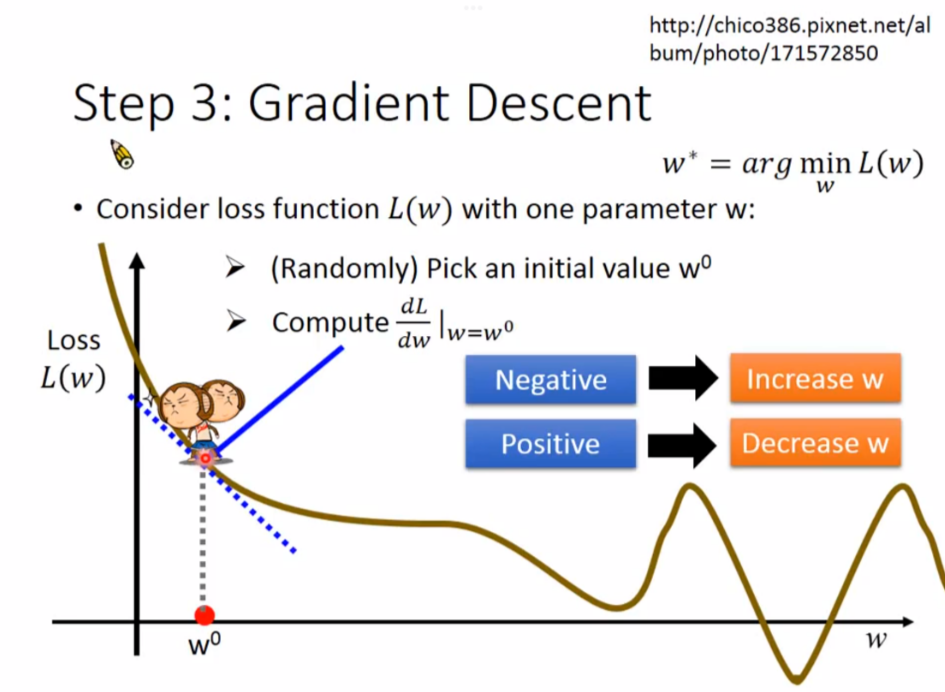 本质上是求斜率,斜率是负数,说明w增加会让L(W)减少,所以要增加w;斜率是正数,说明w增加会让L(w)增加,所以要减少w
本质上是求斜率,斜率是负数,说明w增加会让L(W)减少,所以要增加w;斜率是正数,说明w增加会让L(w)增加,所以要减少w
然而,我们也要w一次需要减多少的问题
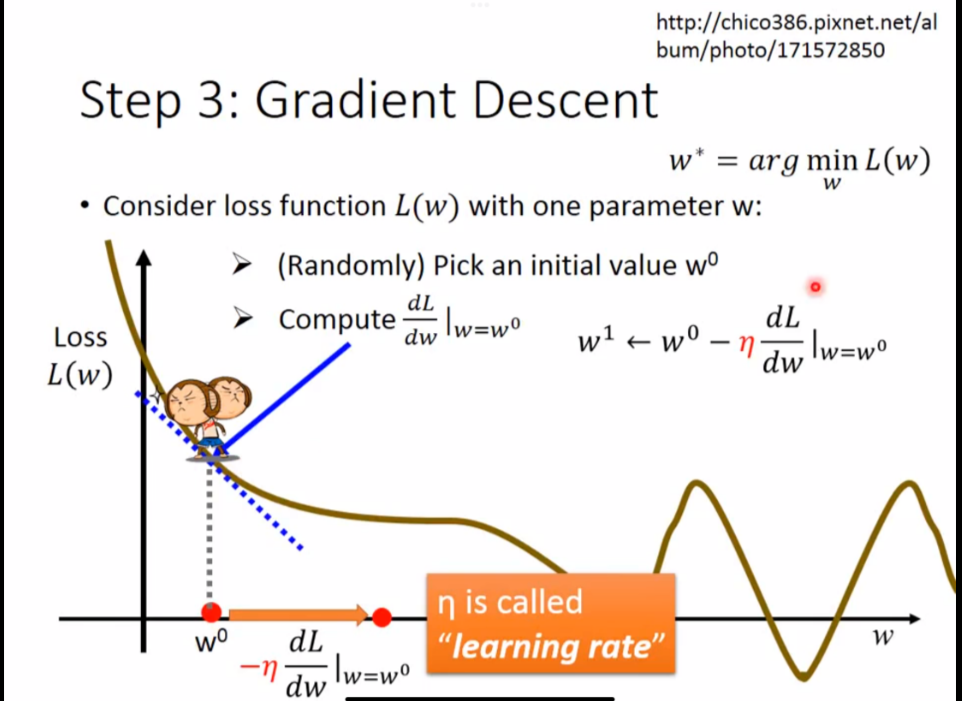 算法如下:
算法如下:
- 随机选一个初始值 $w_{0}$
- 进行一次梯度下降(重复这个步骤,直到斜率为0)
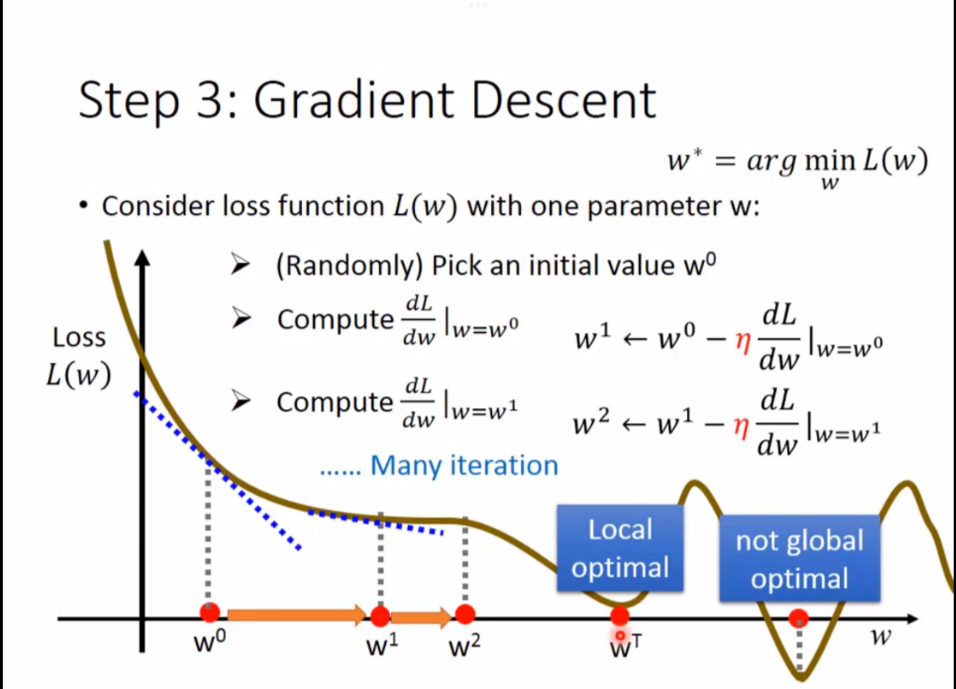 这里有人可能担心,如果达到极值点(Local optimal)而不是最小值点(global optimal)怎么办
这里有人可能担心,如果达到极值点(Local optimal)而不是最小值点(global optimal)怎么办
线性回归(Linear Regression)没有Local optimal
举例:如果有2个参数
其实很类似,就是求斜率变成了求偏导值

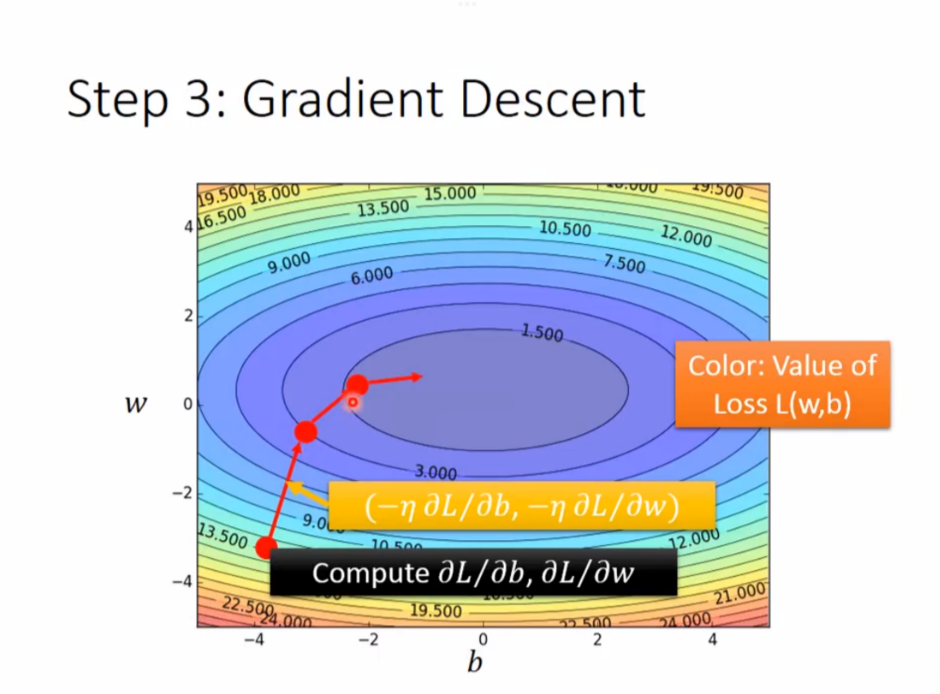
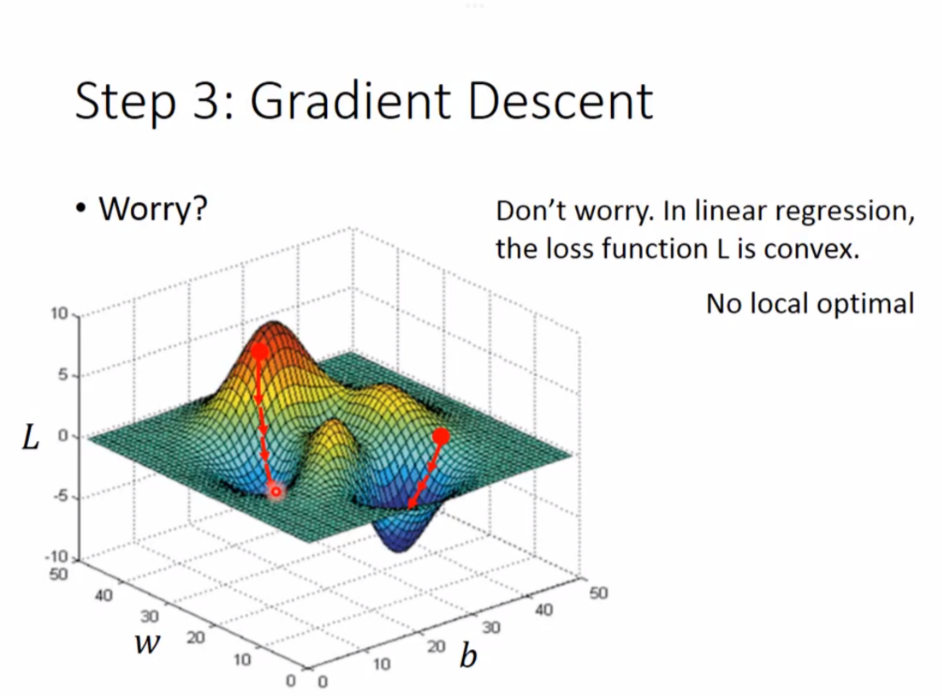
如何做的更好
我们用训练数据训练了一个模型,我们真正关心的是这个模型在未来的预测结果精准度如何
如何做的更好?
1. 更复杂的模型
用更高次幂的函数来替代一开始的模型
然而需要注意的是,并不是模型越复杂越好,太复杂的模型容易造成过拟合(overfitting)(只在训练时效果好,在实际测试时差距很大)
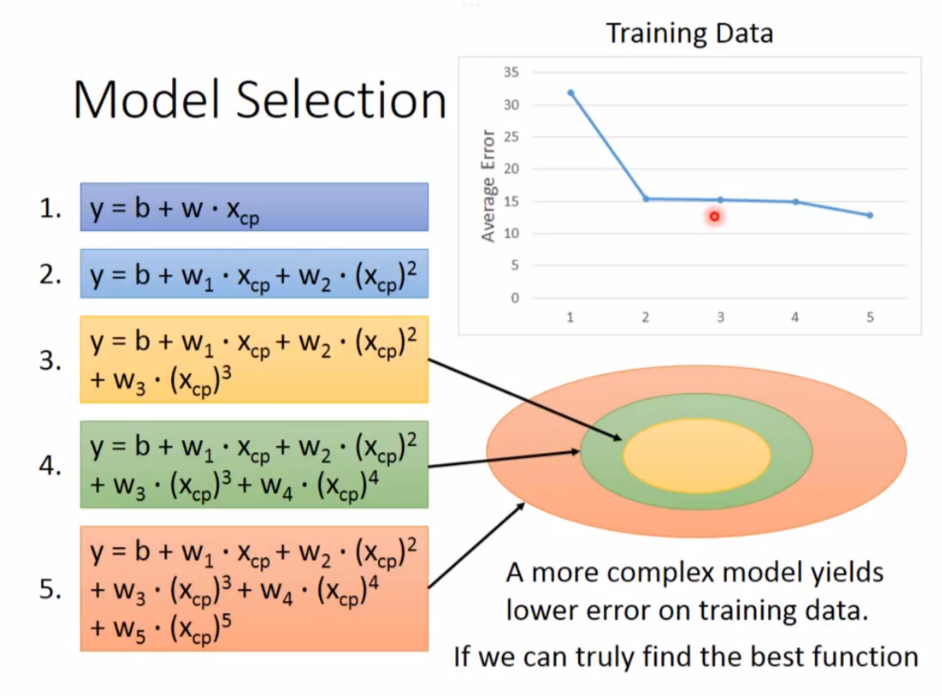

2. 增加训练集,发现隐藏的因子

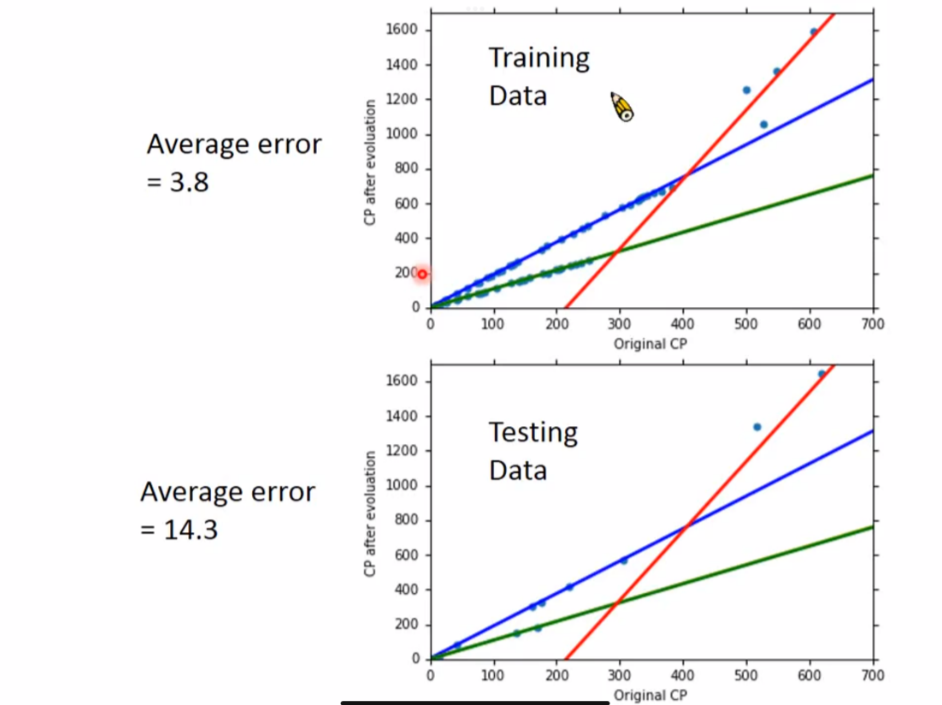
3. Regularization,重新定义更好的Loss Function
 直觉上,w越小越好,因为这代表更加平滑。
直觉上,w越小越好,因为这代表更加平滑。
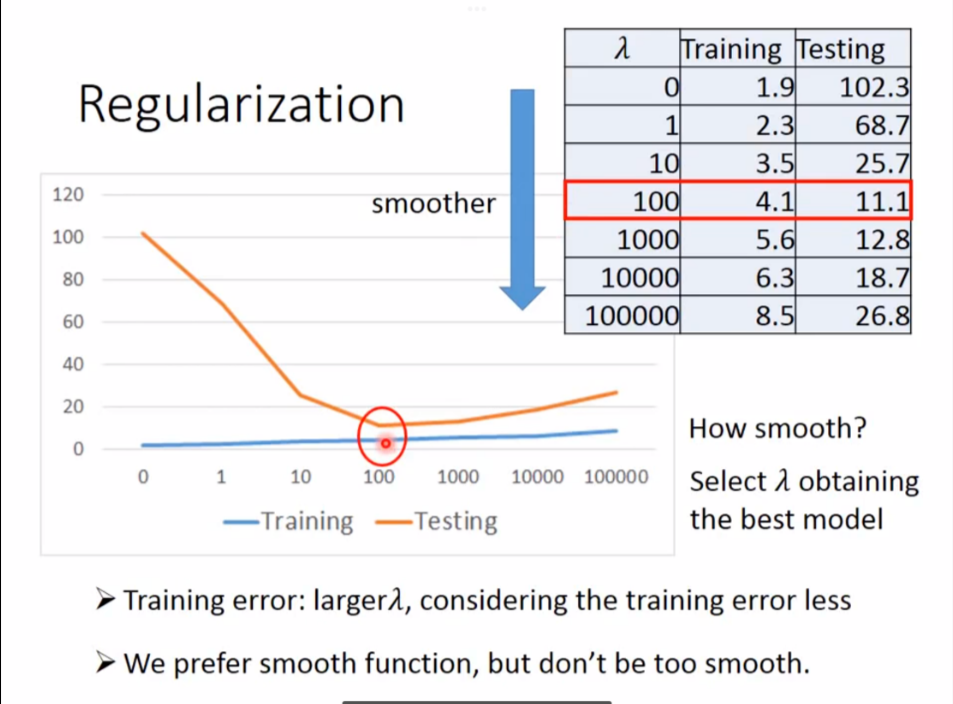 然而也不是越平滑越好,太平滑就是一个直线,这反而没什么意义
然而也不是越平滑越好,太平滑就是一个直线,这反而没什么意义
做Regularization时不考虑bias,因为它只是移动函数位置,不影响平滑程度
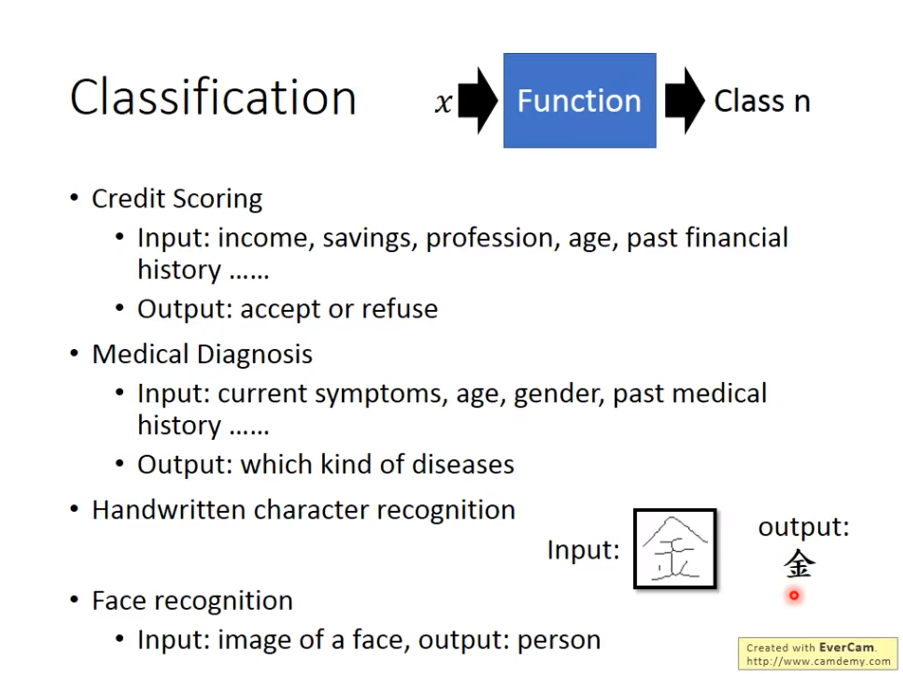
二、Classification: Probabilistic Generative Model
本文主要介绍classification分类,分类是指这样一个函数,输入一个对象x,经过函数之后的输出是这个对象属于哪个类别,比如医疗诊断,把一个病人的年纪性别症状等进行输入,它的输出是具体的哪一种病,比如信用卡借贷系统,把一个人的年纪,收入,职业等输入,输出是=的是系统判定的能否借钱。值得注意的是,在分类函式中,类别是事先已经存在的,只是针对某种输入,它的输出是已有类别中的某一个。
分类问题通常和概率分布函数挂钩
咱们来看些例子:
 拿一个具体的例子来说,我们可以对宝可梦中的精灵进行属性分类。
拿一个具体的例子来说,我们可以对宝可梦中的精灵进行属性分类。
 宝可梦有七种数据,
宝可梦有七种数据,Total、HP、ATK、Defense、SP ATK、SP Defense、Speed。
为了做分类,第一步当然还是收集数据,即宝可梦的数据和属性
当成Regression问题?
有人会问,当成regression问题来做怎么样?
 结果会导致如下情形:
结果会导致如下情形:
1、结果太好反而导致得到的模型不适用
2、在多种种类中,可能并没有相关性,设置成class 1(1),class 2(2),其实是说明class 1和class 2 是有关系的,然而实际上可能并没有关系
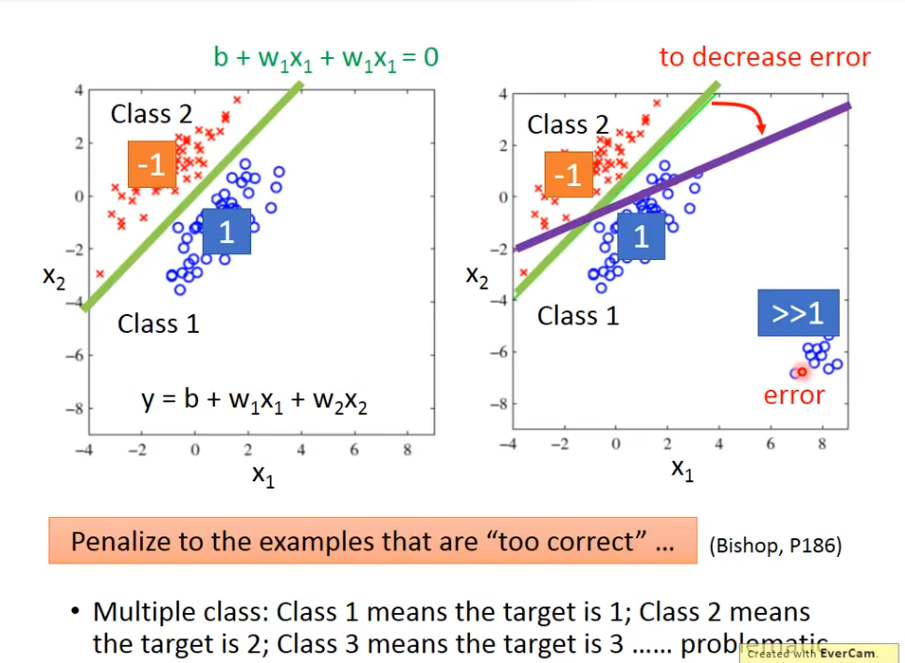
如何处理
其实还是function、Loss function、find best function三步走。只不过Function不再是线性回归了

1. Model
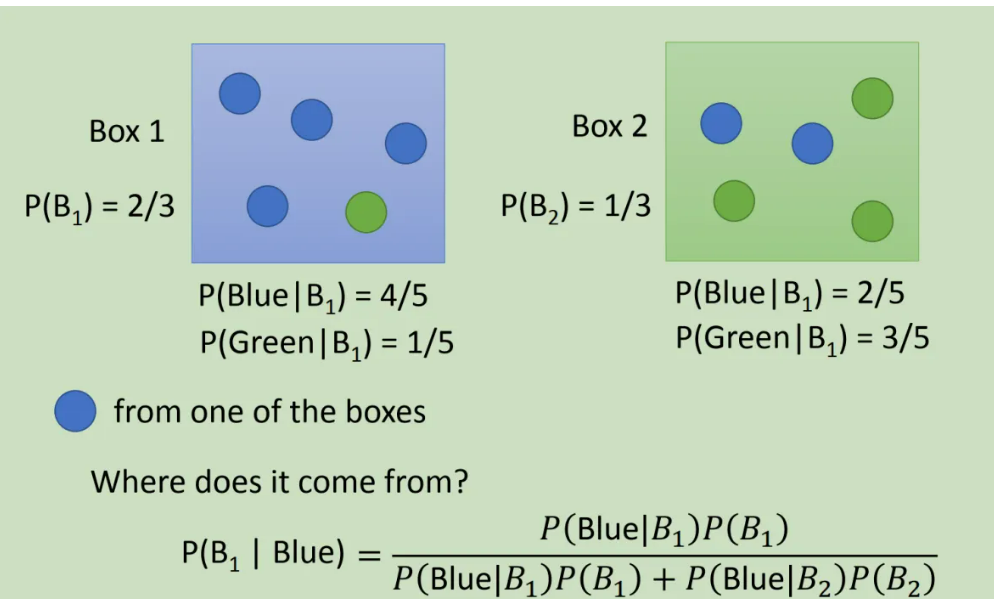 把
把BOX换成Class后
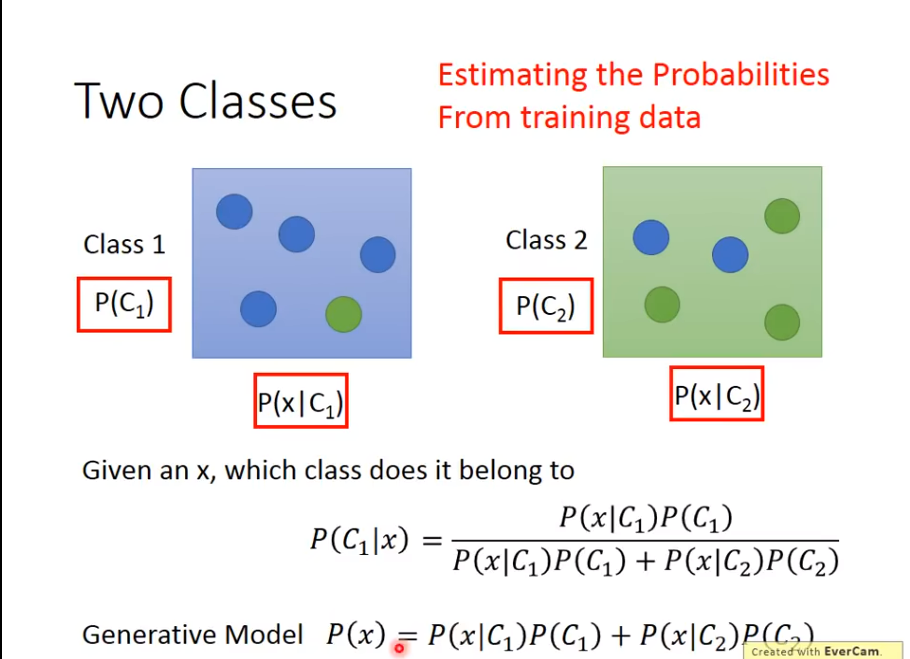 实际上,从样本集当中训练的目的变成了,估算概率
实际上,从样本集当中训练的目的变成了,估算概率
这一整套想法叫做Generative Model
开始实际做一下
 然后就出现了一个问题
然后就出现了一个问题
 如果一个精灵,没有出现在训练集当中,那么它的概率应该如何计算?如果是0,这就是一个垃圾模型,没有意义。
如果一个精灵,没有出现在训练集当中,那么它的概率应该如何计算?如果是0,这就是一个垃圾模型,没有意义。
实际上

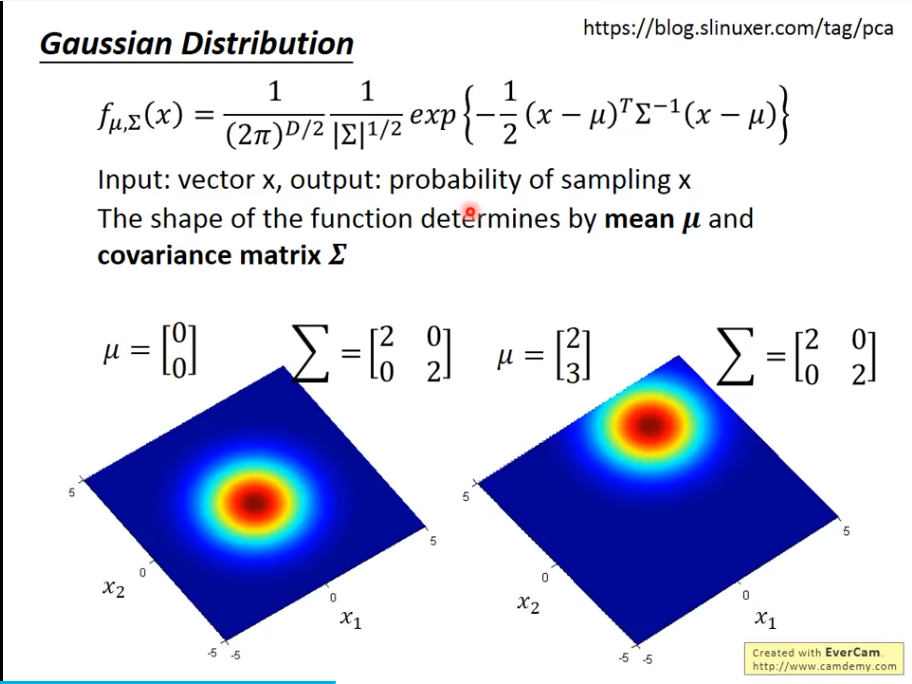 如果我们知道了这两个值
如果我们知道了这两个值mean和 covariance,就可以
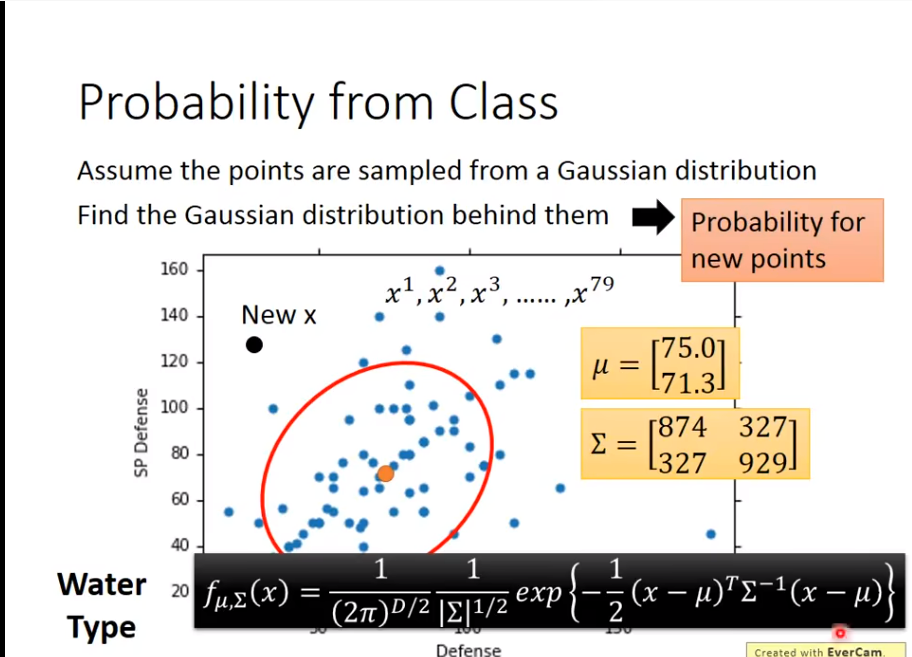 现在的问题就是如何找
现在的问题就是如何找mean和covariance
这里用到了一个Maximum Likelihood的说法
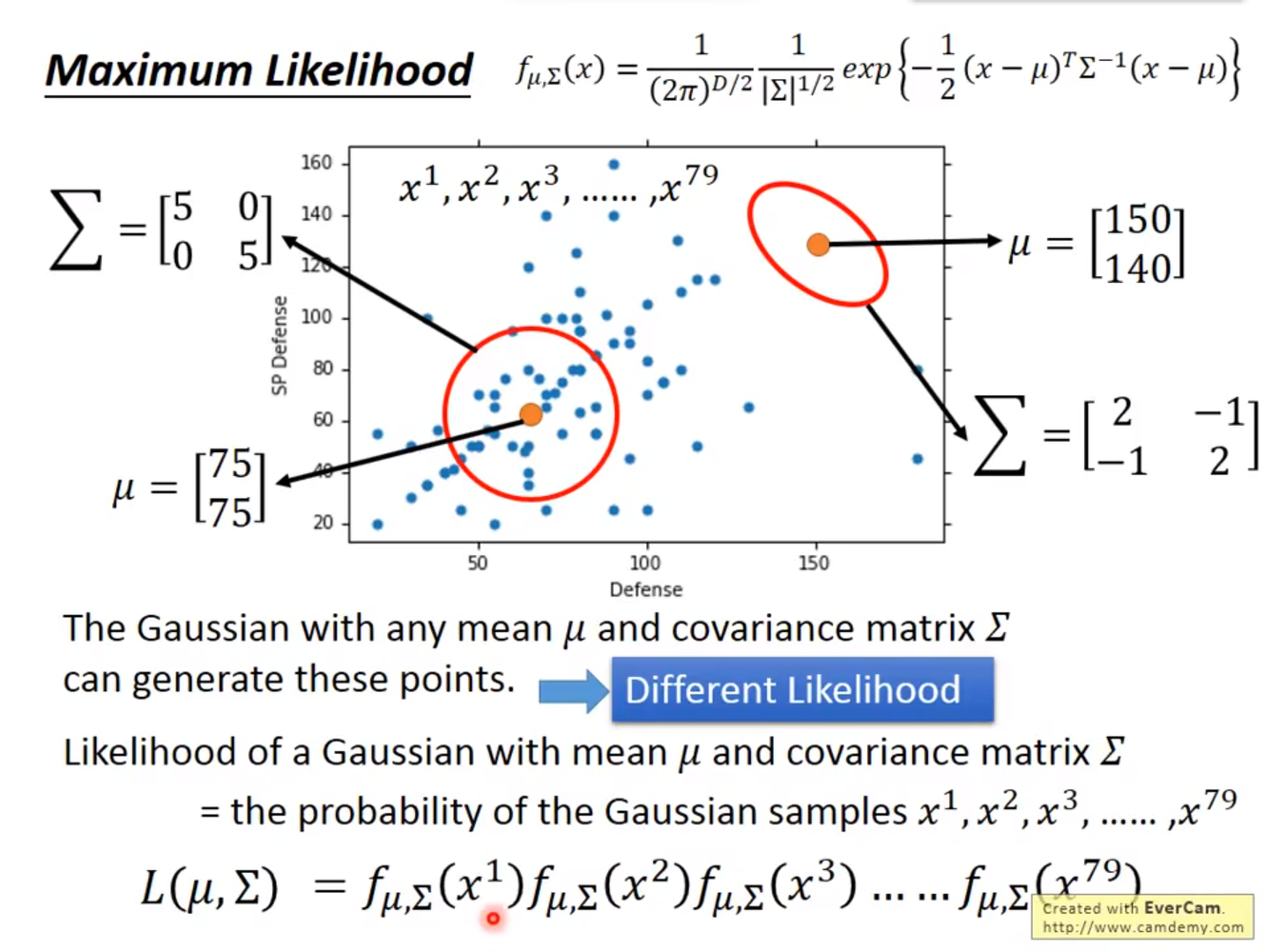

结果如何
那宝可梦水系和一般系举例
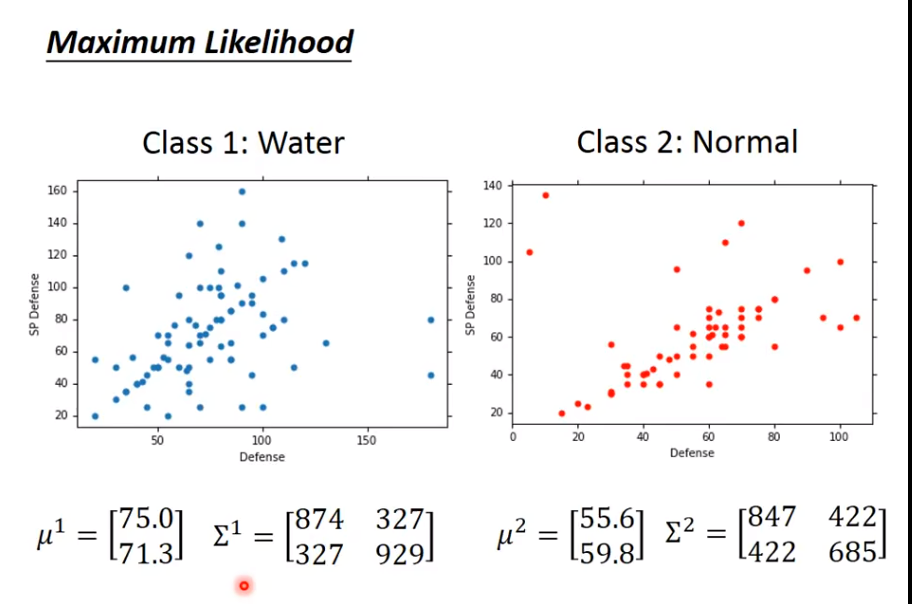
 算完后,得到结果
算完后,得到结果
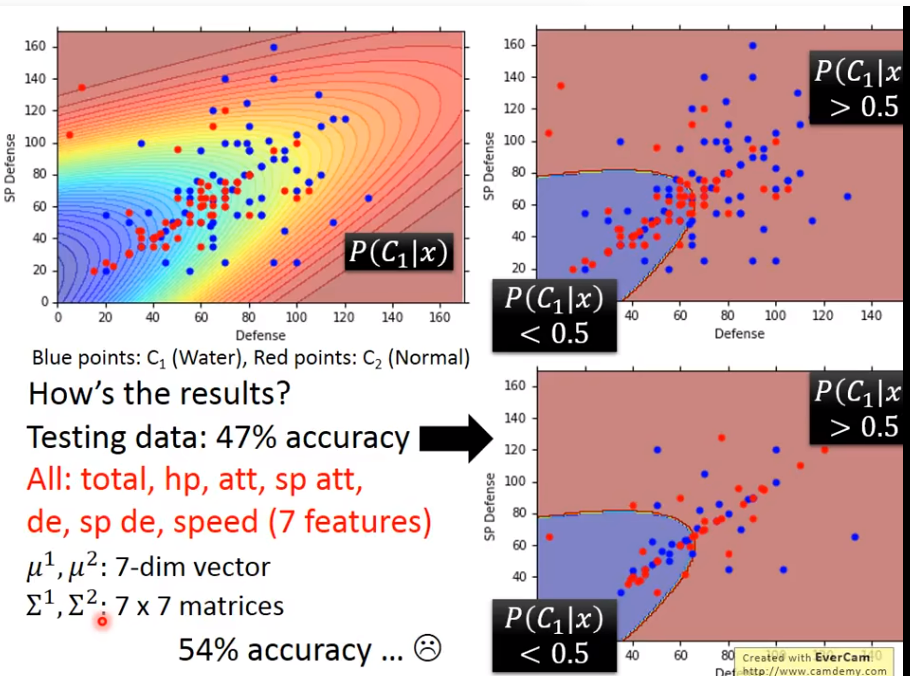 用二维,得到47正确率,然而用了七维,也只有54正确率….
用二维,得到47正确率,然而用了七维,也只有54正确率….
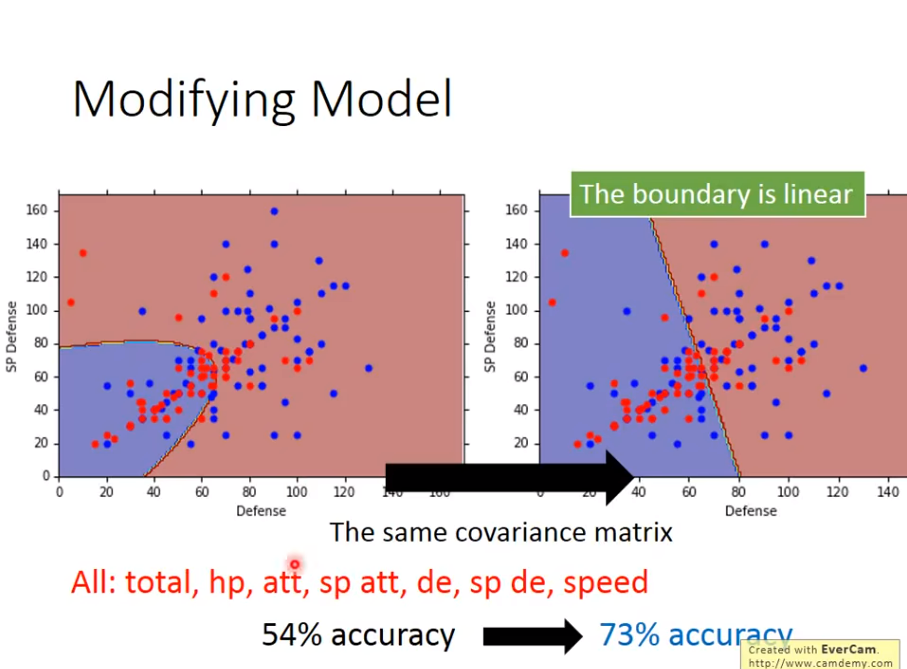
优化:公用同一组covariance
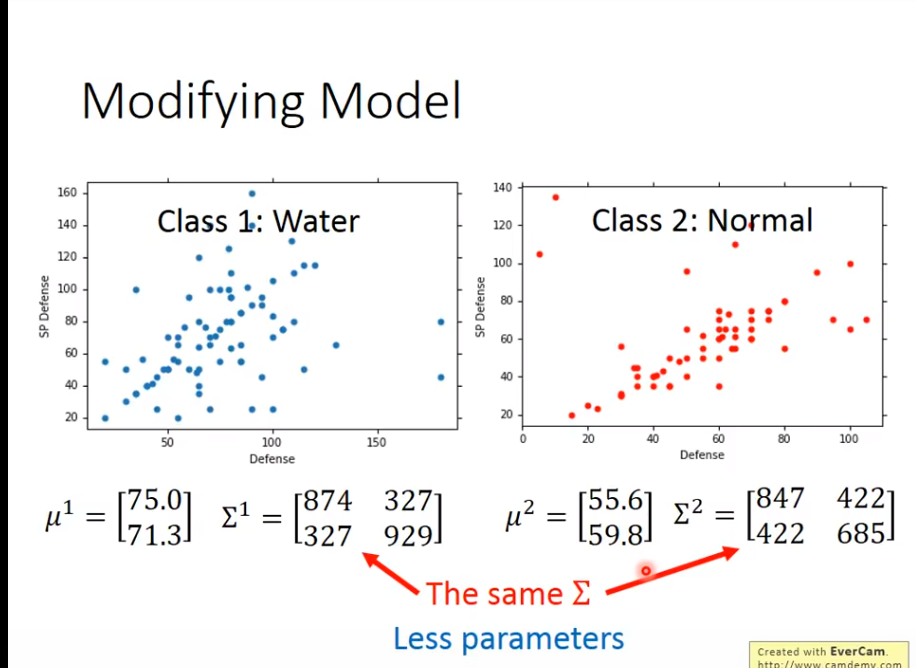 逻辑是,减少参数数量,防止
逻辑是,减少参数数量,防止overfitting
那么公用的covariance是什么呢?
 公用一组
公用一组covariance后,得到结果
2. Loss Function
这里的Loss Function其实就是Likelihood,Likelihood就是Loss Function的一种
3. Best Function
从上述结果里挑选一个Loss最小的Function即为所求
Probability Distribution
为什么要用高斯分布模型?
其实这个是人的智慧,你可以选择你想要的几率分布模型

三、Logistic Regression
使用Posterior Probability(后验概率)进行衡量


大家发现其实好像没必要算啥N1 N2 ...
于是乎,另一种计算概率的方法出现了!
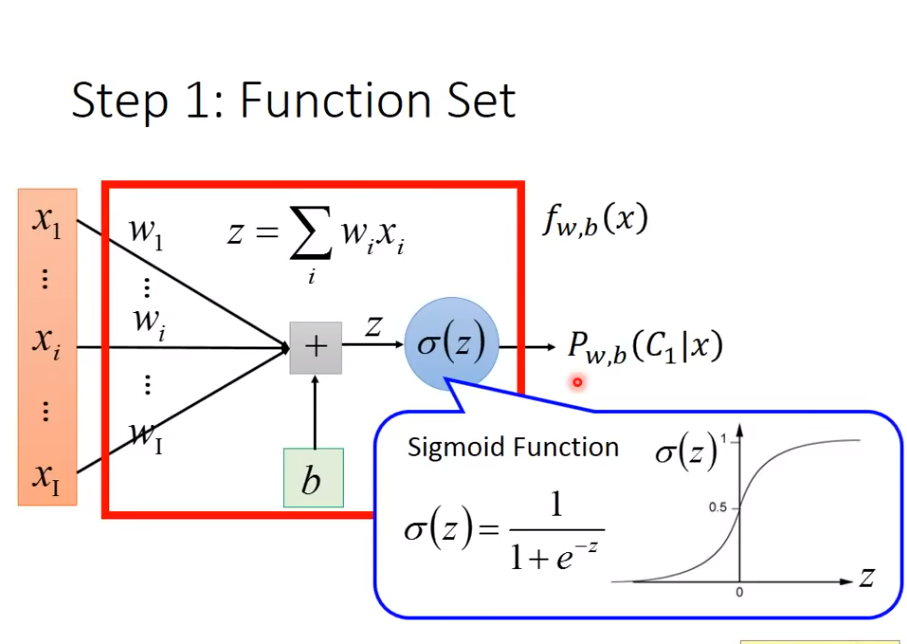
1. Function Set

2. Goodness of Function
 可以看到同样是
可以看到同样是Likelihood的方法

 继续往下算
继续往下算
 可以发现其实结果是
可以发现其实结果是Cross Entrophy(交叉熵)
3. Find the best Function
用gradient descent就可以算了



Logistic Regression VS Linear Regression

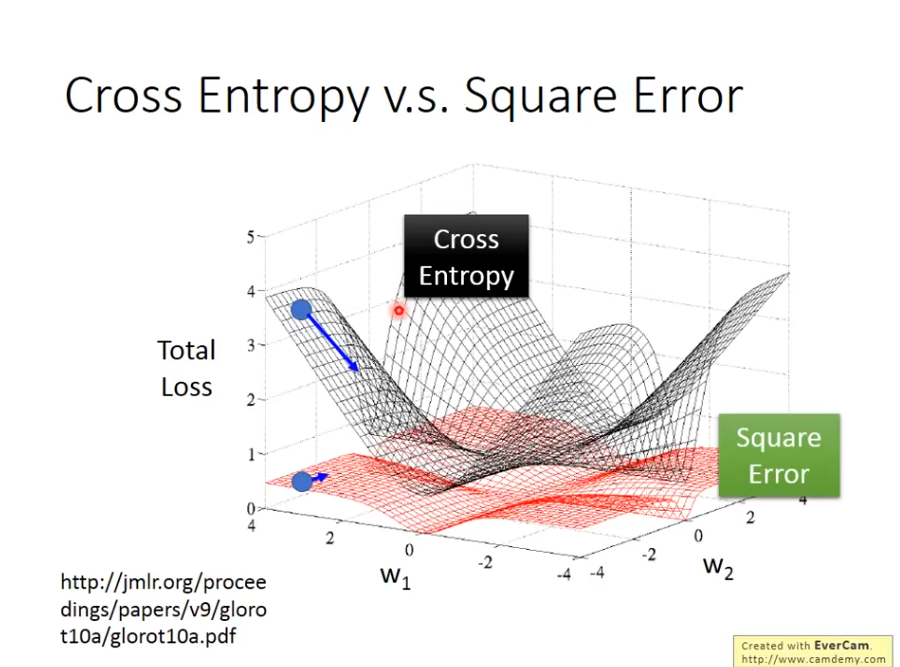
现在问题来了,我们可以用平方差来替代交叉熵吗
答案是不可以
如果用平方差的话,会出现如下问题
 就是在做
就是在做gradient descent时,就算目标距离你很远,微分还是0,这就导致无法逼近目标,导致训练无效
其实logistic regression也被称为Discriminative
 这里,直接找w和b和通过
这里,直接找w和b和通过Generative求各种参数计算出来的是不一样的
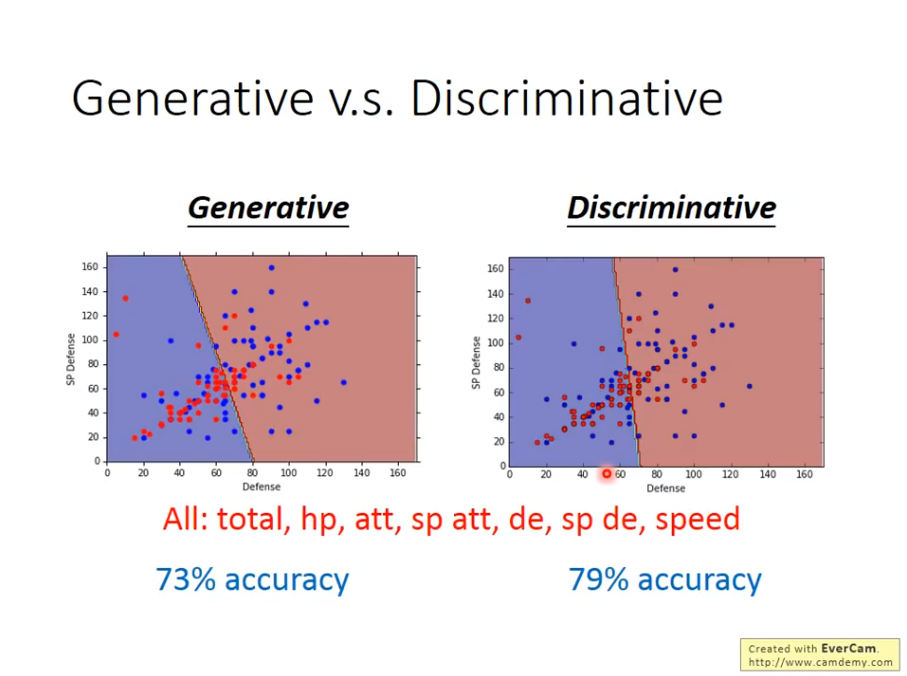 可以看到,
可以看到,Discriminative通常情况下相比于Generative有更高的精确度。
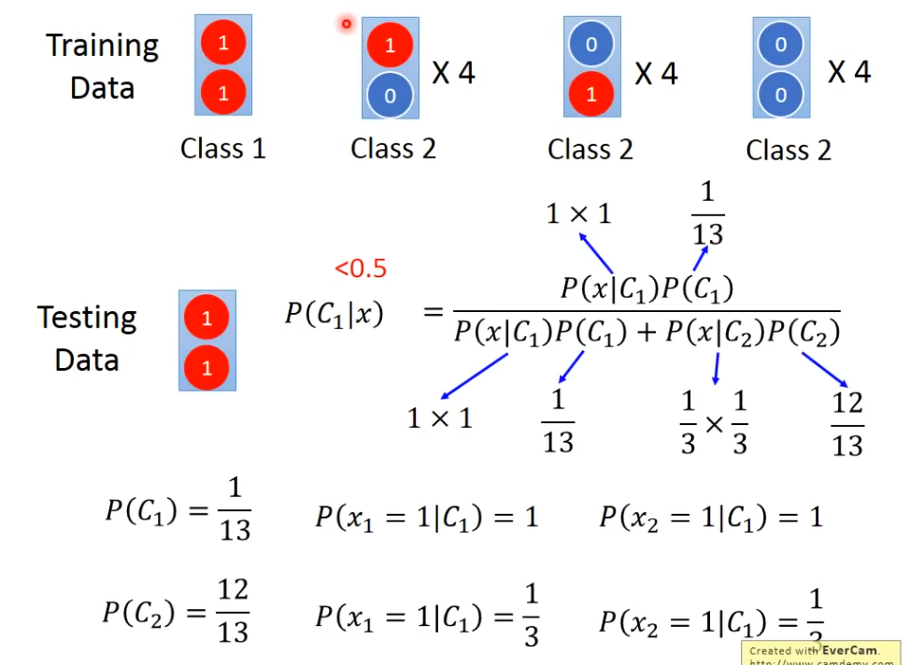
然而,并不是Discriminative就一定好,Generative其实相比于,是做了一些假设的
举个例子

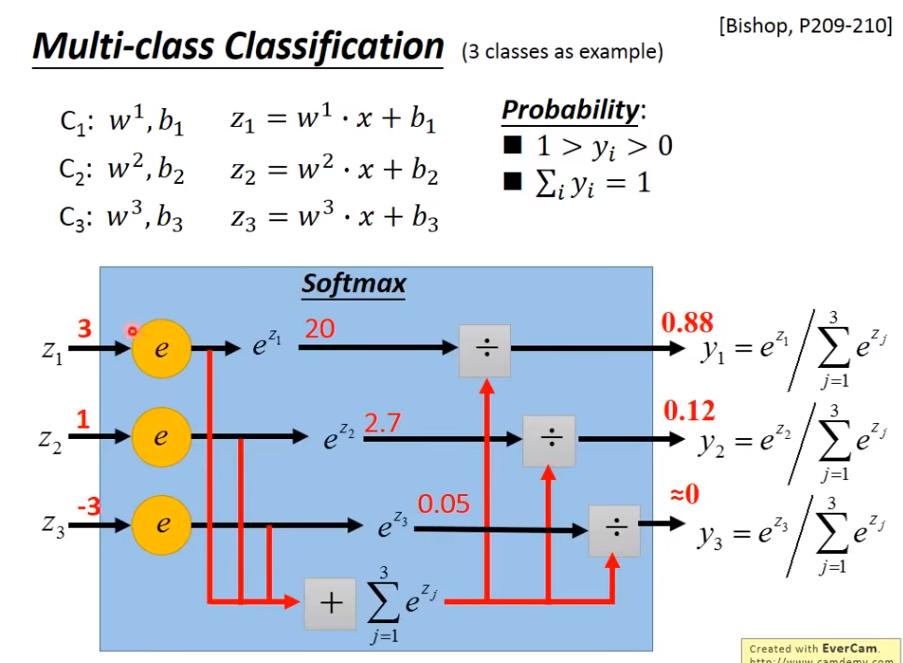
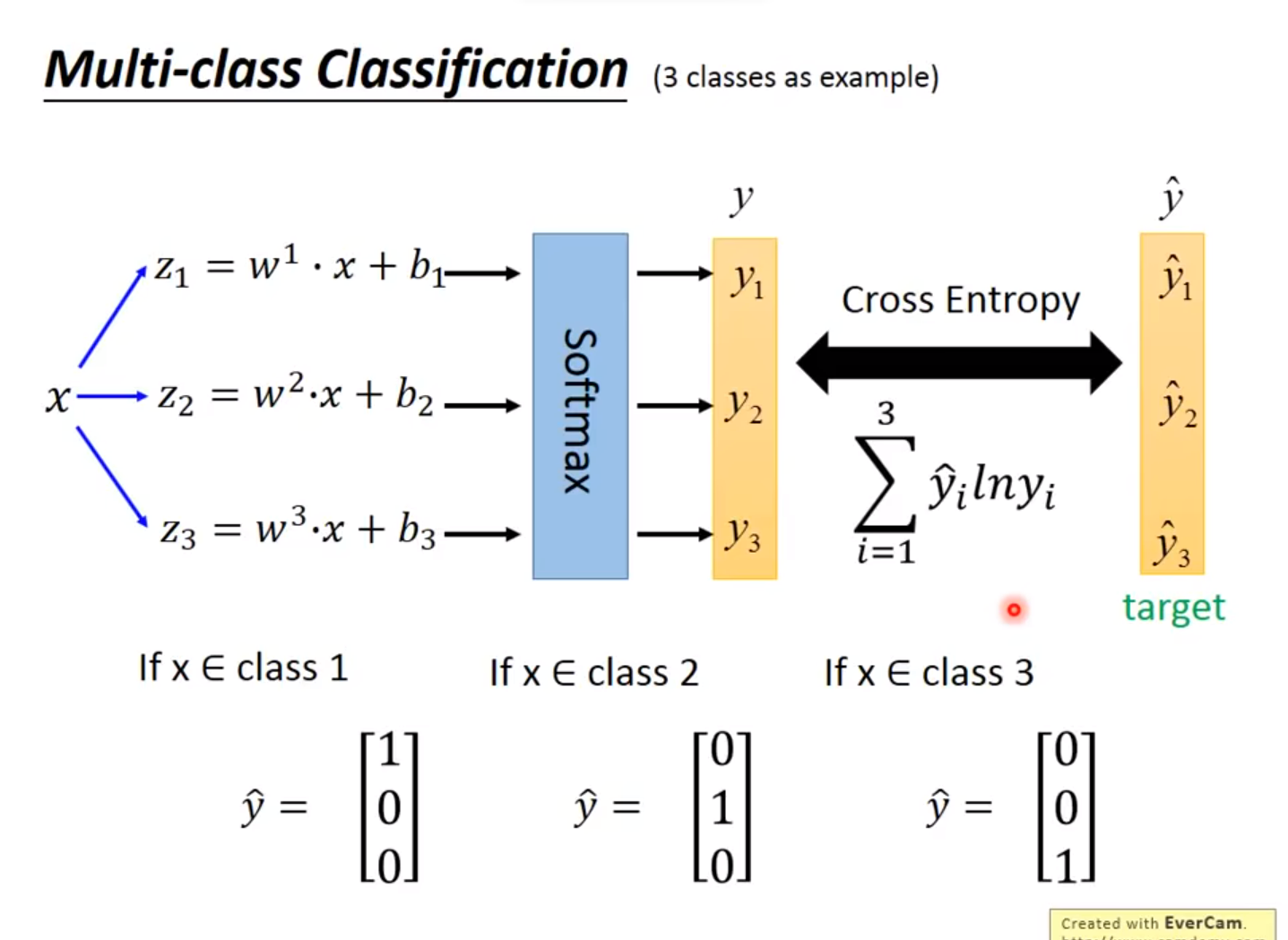
Multi-classification
Limitation Of Logistic Regression
我们发现无法做划出一道线,能够解决问题
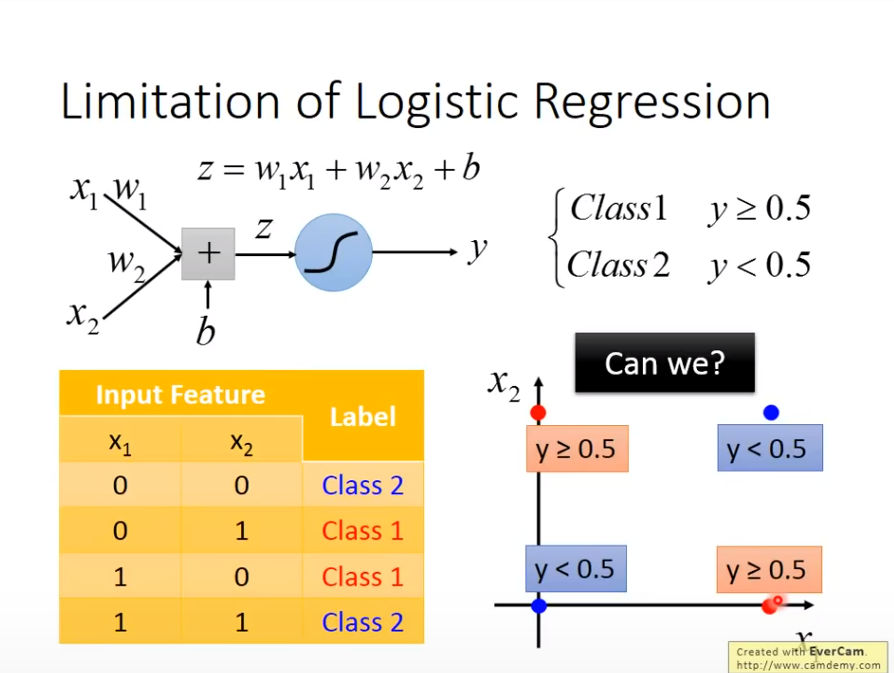
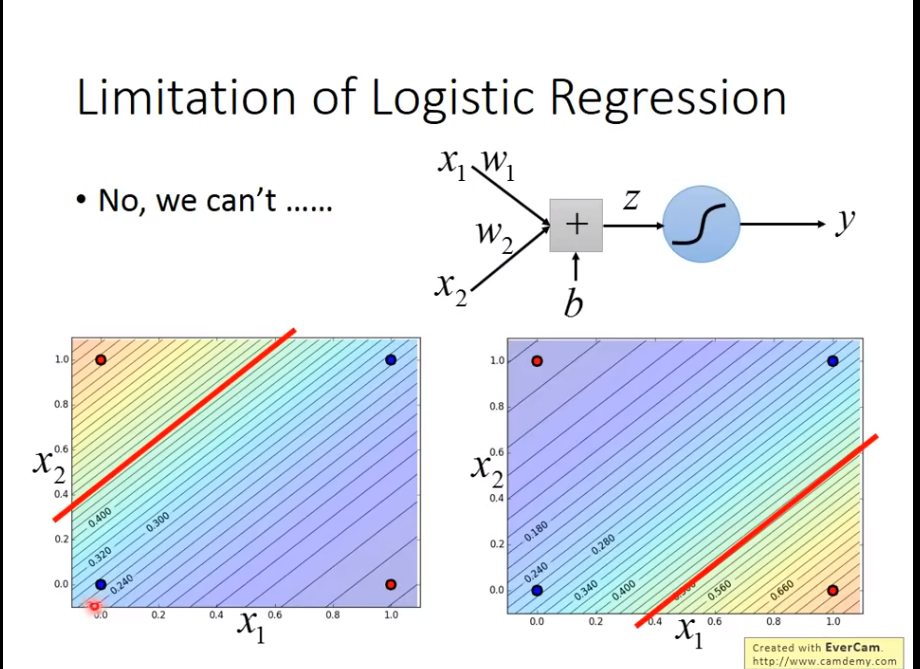
我们使用Transformation
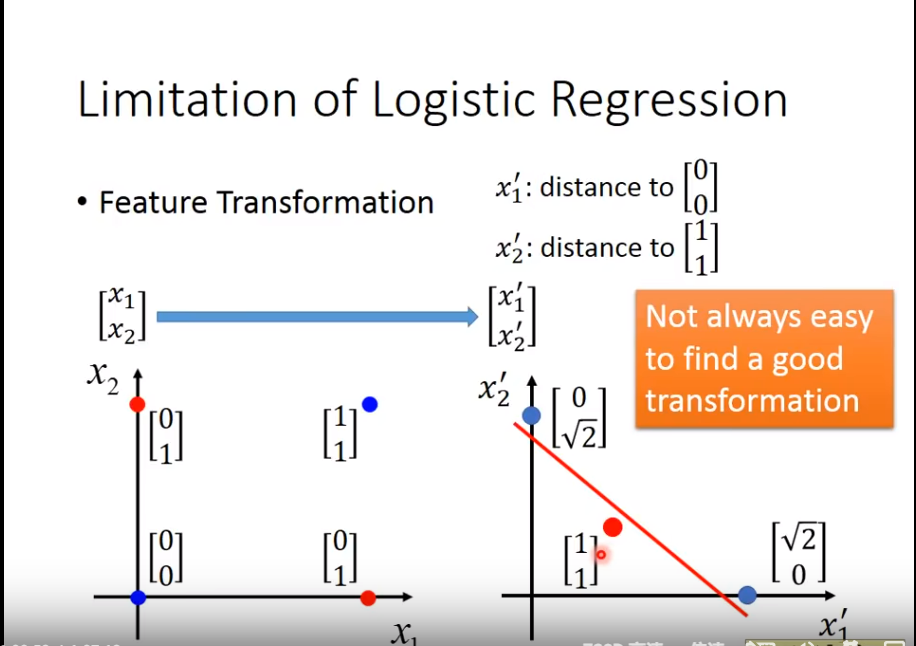 但是,如果
但是,如果Transformation一直是人类来找的,就不是人工智能了,我们希望Transformation是机器自己找的
于是一个很神秘的方法出现了!
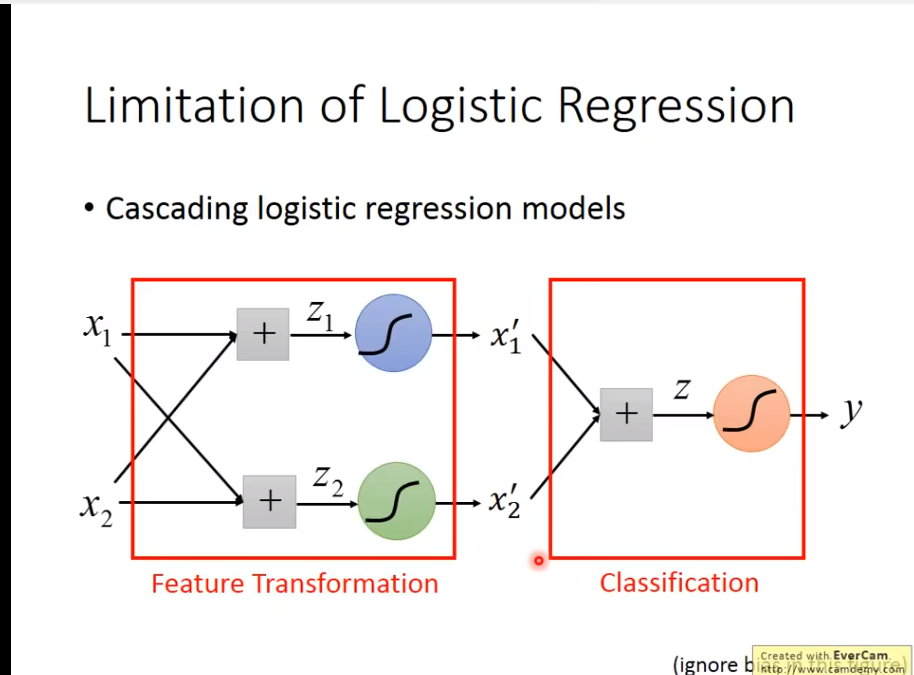
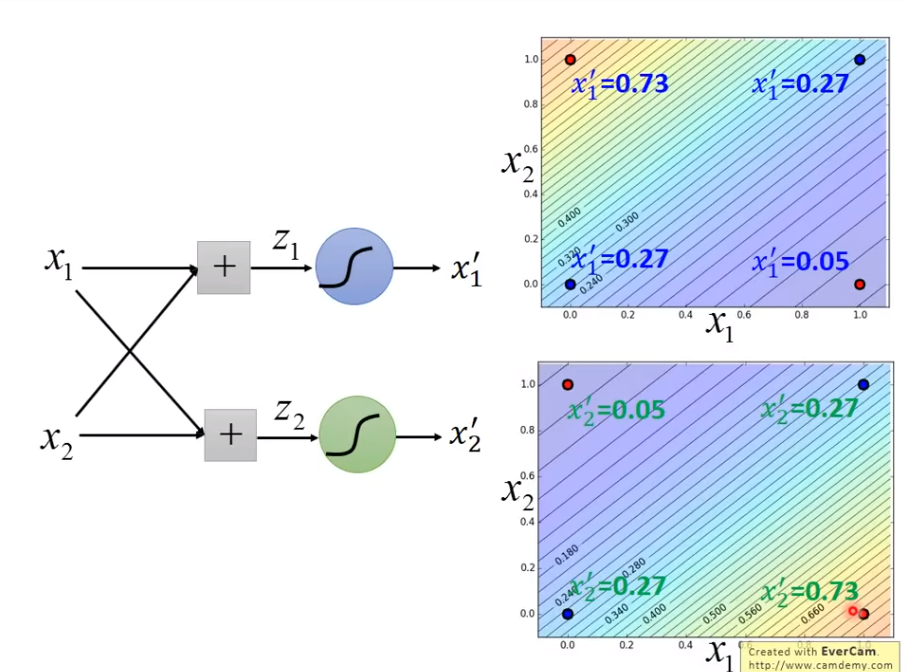
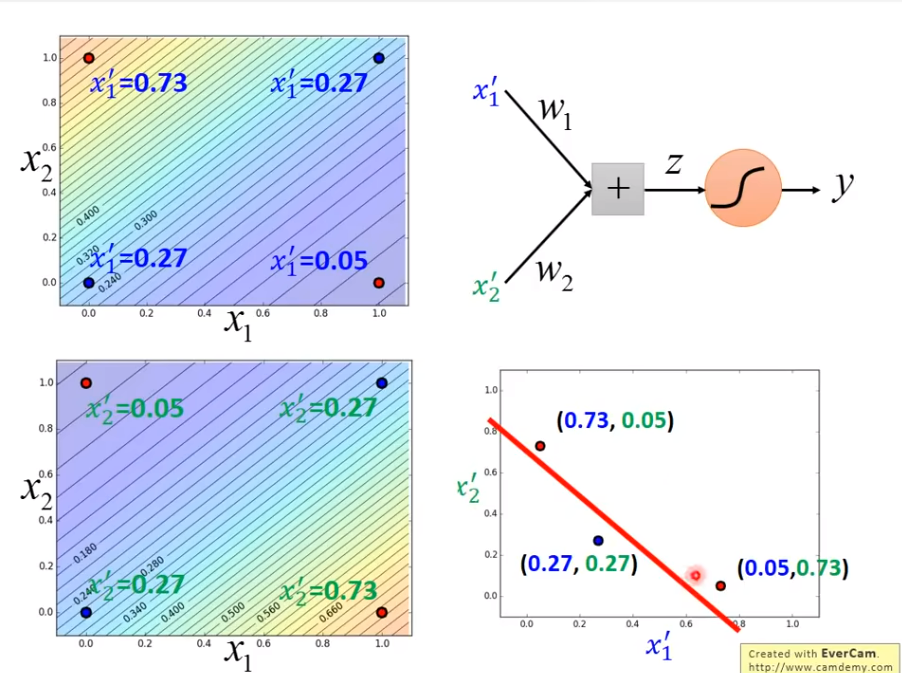
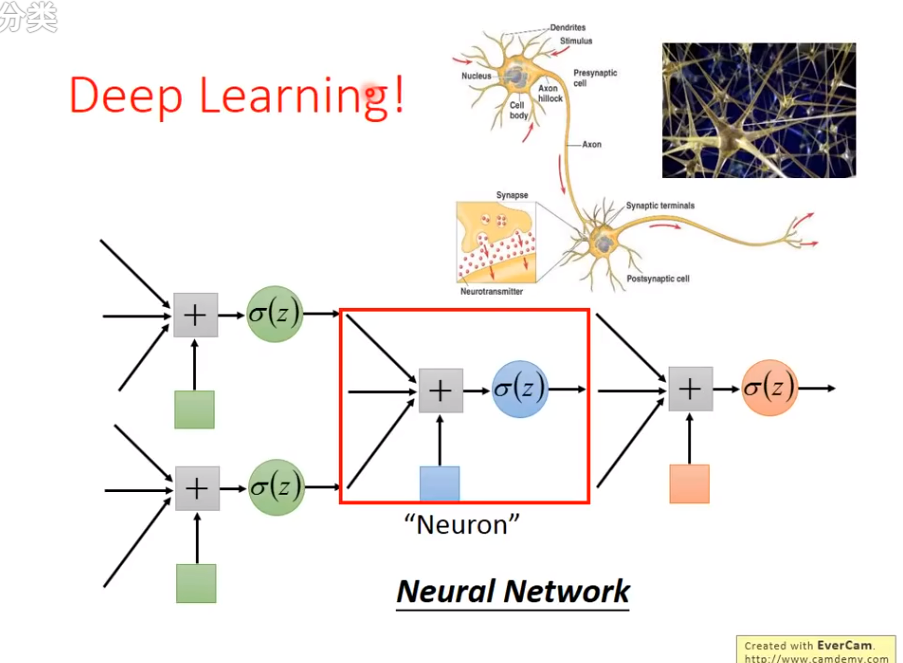
Deep Learning诞生!
这就是Deep Learning的诞生!