Nim游戏
Nim游戏是入门博弈论的很基础的一道题目:
给定N堆物品，第i堆物品有Ai个。两名玩家轮流行动，每次可以任选一堆，取走任意多个物品，可把一堆取光，但不能不取。取走最后一件物品者获胜。两人都采取最优策略，问先手是否必胜
这道题不知道定理的人大概率是看不出来应该怎么做的，许多前人归纳了可能的发生的情况，最终归纳出了很重要的结论（未证明，但是也伪证伪）:
先手必胜的条件是 A1 ^ A2 ^ A3…… ^ An 大于0
sg函数
平日里做的算法题目显然不会那么简单~~
给定N堆物品，第i堆物品有Ai个。两名玩家轮流行动，每次可以任选一堆，取走ki个物品（k1、k2、k3、k4…..kM）。取走最后一件物品者获胜。两人都采取最优策略，问先手是否必胜。
显然这道题目就不能单纯用nim游戏那个规律来做了。
聪明的前人发现（前人真的是太牛啦），可以用有向图来模拟这种游戏的局势。
mex函数
mex函数定义为 不存在集合中的最小非负整数。(集合必须满足所有值都是非负整数)
举个例子，mex({0,1,3})=2,mex({1,2,3,4})=0
大家可能觉得现在引入mex函数有点突兀，但是不要紧，先记住
有向图
聪明的前人发现，博弈的本质是一个有向图游戏，如图所示：
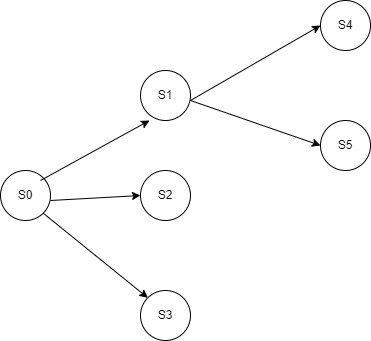其中，S0指的是游戏的初始状态，S1,S2,S3是在玩家进行了某些动作后得到的新状态（显然玩家此时只能做3个不同的动作），S4,S5是S1在玩家进行了某些动作后得到的新状态。
于此同时 定义 SG(S0)=mex({SG(S1),SG(S2),SG(S3)})
SG(S1)=mex({SG(S4),SG(S5)})
在当前状态没有跟后续状态时，SG(S2)=SG(S3)=SG(S4)=SG(S5)=0
有了有向图和mex函数后，我们就可以解决较难的博弈问题了。
有N堆物品，说明初始状态中有N个子游戏，而有M个可选操作，说明有M个可走的策略，此时又来了一个非常重要的结论：如果一个状态S中的N个子游戏互相独立，即互不影响，则SG(S)=SG(N1) ^ SG(N2) ^ SG(N3)…. ^ SG(NN)
该题中，N堆物品说明了有N个独立的子游戏。
一般思路
- 读入N堆物品后，分别求出 只有Ni堆 时的 SG函数值 SG（Ni）
- 求出 SG(N1) ^ SG(N2) ^ SG(N3) ^ … ^ SG(Nn)
重点在于如何求SG(Ni)
- SG(Ni) = mex（{SG(M1),SG(M2),SG(M3),…SG(Mm)}）,Mi代表在选择M个策略中的其中之一后，游戏进入的另一个状态，可以使用递归的函数调用来计算
- 在集合中找到不属于其中的最小非负整数x，SG(Ni)=x.(方便时可以直接枚举)